YTEP-0011: Symbol units in yt¶
Abstract¶
This YTEP describes adding symbolic units to yt using the sympy package. The
main benefit is to make sure units are carried through calculations in a
transparent and intuitive manner. The new components are:
- a
Unitclass, which describes the dimensionality (powers of mass, length, time, temperature) and conversion factor of any unit.- a
UnitRegistryclass, which stores valid atomic unit symbols (ex: “g” for gram).- a
YTArrayclass, a subclass of NumPyndarraythat attaches aUnitobject.- a
YTQuantityclass, a subclass of YTArray which is restricted to a single element (for handling scalars).
Status¶
Completed
Project Management Links¶
The code can be found in the unit refactor pull request:
https://bitbucket.org/yt_analysis/yt/pull-request/662/unit-refactor/diff#comment-897255
The latest work is in Matt Turk’s fork in yt in the unitrefactor bookmark:
https://bitbucket.org/MatthewTurk/yt/commits/branch/unitrefactor
The work is based on Casey’s dimensionful library:
Detailed Description¶
Background¶
The current system for units is functional but not terribly flexible.
All data are treated as scalars and it is up to the user to convert data from
CGS, which yt uses internally, to their chosen unit system. A sample workflow
might look like this:
from yt.mods import *
from yt.utilities.physical_constants import mass_sun_cgs
pf = load('IsolatedGalaxy/galaxy0030/galaxy0030')
dd = pf.h.all_data()
mass = dd['CellMass']
print "Mass in CGS: ", mass
print "Mass in Solar Masses: ", dd['CellMass']/mass_sun_cgs
print "Mass in code units: ", dd['CellMass']/pf['Mass']
This model works well if a user always uses CGS units. If the user needs a quantity in a different unit system, they run into trouble. This is illustrated above in the example to convert to ‘solar mass’ units, since this isn’t a proper unit, the conversion isn’t stored inside the pf dict, so a user will either need to import the unit definition from yt, or add their own definition to their script. The situation is a little bit better for length conversions:
dx = dd['dx']
print "Cell dx in code units: ", dx
print "Cell dx in centimeters: ", dx*pf['Length']
print "Cell dx in megaparsecs: ", dx*pf['mpc']
This works pretty nicely, since all of the various length units are stored in the pf dictionary. However, this example illustrates another problem; here dx is returned in code units, while most quantities are returned in CGS. If we wanted to enforce that all quantities be returned in CGS, we would need to painstakingly go through the codebase, tweaking the field definitions and places where fields are used so that units are handled properly. Clearly, a better solution is needed.
Cosmological units are also handled in a somewhat ad hoc way. Each of the code frontends need to detect that a simulation was performed using comoving units, and define new scaled, comoving and scaled comoving units (i.e. ‘kpccm’, ‘kpchcm’ and ‘kpch’). This encourages duplication of code in each of the frontends and makes likely that different frontends will ignore some of the cosmological units that are defined in the Enzo frontend. In addition, this is not documented in the frontend docs, making it easier for newly supported codes to miss this. Cosmological units are also not labeled correctly in plots.
To ensure units to display nicely on plots, the unit definition is currently encoded as a raw string in LaTeX format:
add_field("MagneticEnergy",function=_MagneticEnergy,
units=r"\rm{ergs}\/\rm{cm}^{-3}",
display_name=r"\rm{Magnetic}\/\rm{Energy}")
This is harmful for readability and has the effect that user-defined or automatically generated fields are not assigned units.
Proposed Solution¶
We propose to handle units in a more automatic fashion, leveraging the symbolic
math library sympy. Instead of returning a NumPy ndarray when users query
for fields, the __getitem__ selector on data objects will return a
YTArray, a subclass of ndarray. This preserves ndarray’s array
operations, including deep and shallow copies, broadcasting, and views.
Additonally, YTArray has a Unit object attached to it that tracks units
associated with each value in the array. This is encoded in the __repr__
method of YTArray:
>>> dd['density']
YTArray([ 4.92775113e-31, 4.94005233e-31, 4.93824694e-31, ...,
1.12879234e-25, 1.59561490e-25, 1.09824903e-24]) g/cm**3
YTArray defines several user-visible member functions:
convert_to_unitsConverts an array to a valid unit, specified by a string argument. Valid units possess the same
dimensionexpression as the current unit.convert_to_cgsConverts the array to CGS units.
in_unitsReturns a copy of the array in a valid unit, specified by a string argument. Valid units possess the same
dimensionexpression as the current unit.in_cgsReturns a copy of the array in CGS units.
It’s important to remember that convert_to_cgs and convert_to_units do
in-place conversion of an existing array and in_units and in_cgs return
a copy of the original array in the new unit. This can get complicated if one
isn’t careful about the distinction between creating copies and references, as
illustrated in the following example:
>>> dens = dd['density']
>>> print dens
[ 4.92775113e-31 4.94005233e-31 4.93824694e-31 ..., 1.12879234e-25
1.59561490e-25 1.09824903e-24] g/cm**3
>>> dens.convert_to_units('Msun/pc**3')
>>> print dens
[ 7.27920765e-09 7.29737882e-09 7.29471191e-09 ..., 1.66743685e-03
2.35702085e-03 1.62231868e-02] Msun/pc**3
>>> dd['density'].in_units('Msun/pc**3')
YTArray([ 7.27920765e-09, 7.29737882e-09, 7.29471191e-09, ...,
1.66743685e-03, 2.35702085e-03, 1.62231868e-02]) Msun/pc**3
In the example above, if a user tries to query dd['density'] again, they
will find that it has been converted to solar masses per cubic parsec, since a
shallow copy, dens, underwent an in-place unit conversion. In practice this
is not a big concern, since the unit metadata is preserved and the array values
are still correct in the new unit system, all numerical operations will still be
correct.
One of the nicest aspects of this new unit system is that the symbolic algebra for unitful operations is performed automatically by sympy:
>>> print dd['cell_mass']/dd['cell_volume']
[ 4.92775113e-31 4.94005233e-31 4.93824694e-31 ..., 1.12879234e-25
1.59561490e-25 1.09824903e-24] g/cm**3
>>> print dd['density']
[ 4.92775113e-31 4.94005233e-31 4.93824694e-31 ..., 1.12879234e-25
1.59561490e-25 1.09824903e-24] g/cm**3
YTArray is primarily useful for attaching units to NumPy ndarray
instances. For scalar data, we have created the new YTQuantity class. In
the proposed implementation, YTQuantity is a subclass of YTArray with
the requirement that it is limited to one element. YTQuantity is primarily
useful for physical constants and ensures that the units are propogated
correctly when composing quantities from arrays, physical constants, and
unitless scalars:
>>> from yt.utilities.physical_constants import boltzmann_constant
>>> print dd['temperature']*boltzmann_constant
[ 1.28901607e-12 1.29145540e-12 1.29077208e-12 ..., 1.63255263e-12
1.59992074e-12 1.40453862e-12] erg
With this new capability, we will have no need for fields defined only to handle
different units (e.g. RadiusCode, Radiuspc, etc.). Instead, there will
only be one definition and if a user needs the field in a different unit system,
they can quickly convert using convert_to_units or in_units.
When a StaticOutput object is instantiated, it will its self instantiate and
set up a UnitRegistry class that contains a full set of units that are
defined for the simulation. This is particularly useful for cosmological
simulations, since it makes it easy to ensure cosmological units are defined
automatically.
The new unit systems lets us to encode the simulation coordinate system and scaling to physical coordinates directly into the unit system. We do this via “code units”.
Every StaticOutput object will have a length_unit, time_unit,
mass_unit, and velocity_unit attribute that the user can quickly and
easily query to discover the base units of the simulation. For example:
>>> from yt.mods import *
>>> ds = load("Enzo_64/DD0043/data0043")
>>> print ds.length_unit
128 Mpccm/h
Additionally, we will allow conversions to coordinates int the simulation
coordinate system defined by the on-disk data. Data in code units will be
available by converting to code_length, code_mass, code_time,
code_velocity, or any combination of those units. Code units will preserve
dimensionality: an array or quantity that has units of cm will be
convertible to code_length, but not to code_mass.
On-disk data will also be available to the user, presented in unconverted code units. To obtain on-disk data, a user need only query a data object using an on-disk field name:
>>> from yt.mods import *
>>> ds = load("Enzo_64"/DD0043/data0043")
>>> dd = ds.h.all_data()
>>> print dd['Density']
[ 6.74992726e-02 6.12111635e-02 8.92988636e-02 ..., 9.09875931e+01
5.66932465e+01 4.27780263e+01] code_mass/code_length**3
>>> print dd['density']
[ 1.92588950e-31 1.74647714e-31 2.54787551e-31 ..., 2.59605835e-28
1.61757192e-28 1.22054281e-28] g/cm**3
Here, the first data object query is returned in code units, while the second is
returned in CGS. This is because Density is an on-disk field, while
density is a ‘standard’ yt field. See YTEP-0003: Standardizing field names.
Unit labels for plots will be programatically generated. This will leverage the sympy LaTeX output module. Even though the field definitions will have their units encoded in plain text, we will be able to automatically generate LaTeX to supply to matplotlib’s mathtext parser.
Implementation¶
Our unit system has 6 base dimensions, mass, length, time,
temperature, metallicity, and angle. The unitless dimensionless
dimension, which we use to represent scalars is also technically a base
dimension, although a trivial one.
For each dimension, we choose a base unit. Our system’s base units are grams, centimeters, seconds, Kelvin, metal mass fraction, and radian. All units can be described as combinations of these base dimensions along with a conversion factor to equivalent base units.
The choice of CGS as the base unit system is somewhat arbitrary. Most unit
systems choose SI as the reference unit system. We use CGS to stay consistent
with the rest of the yt codebase and to reflect the standard practice in
astrophysics. In any case, using a physical coordinate system makes it
possible to compare quantities and arrays produced by different datasets,
possibly with different conversion factors to CGS and to code units. We go into
more detail on this point below.
We provide sympy Symbol objects for the base dimensions. The dimensionality
of all other units should be sympy Expr objects made up of the base
dimension objects and the sympy operation objects Mul and Pow.
Let’s use some common units as examples: gram (g), erg (erg), and solar
mass per cubic megaparsec (Msun / Mpc**3). g is an atomic, CGS base
unit, erg is an atomic unit in CGS, but is not a base unit, and
Msun/Mpc**3 is a combination of atomic units, which are not in CGS, and one
of them even has a prefix. The dimensions of g are mass and the cgs
factor is 1. The dimensions of erg are mass * length**2 * time**-2
and the cgs factor is 1. The dimensions of Msun/Mpc**3 are mass /
length**3 and the cgs factor is about 6.8e-41.
We use the UnitRegistry class to define all valid atomic units. All unit
registries contain a unit symbol lookup table (dict) containing the valid
units’ dimensionality and cgs conversion factor. Here is what it would look
like with the above units:
{ "g": (mass, 1.0),
"erg": (mass * length**2 * time**-2, 1.0),
"Msun": (mass, 1.98892e+33),
"pc": (length, 3.08568e18), }
Note that we only define atomic units here. There should be no operations in
the registry symbol strings. When we parse non-atomic units like
Msun/Mpc**3, we use the registry to look up the symbols. The unit system in
yt knows how to handle units like Mpc by looking up unit symbols with and
without prefixes and modify the conversion factor appropriately.
We construct a Unit object by providing a string containing atomic unit
symbols, combined with operations in Python syntax, and the registry those
atomic unit symbols are defined in. We use sympy’s string parsing features to
create the unit expression from the user-provided string. Here’s how this works
on Msun/Mpc**3:
>>> from sympy.parsing.sympy_parser import parse_expr
>>> unit_expr = parse_expr("Msun/Mpc**3")
>>> from sympy.printing import print_tree
>>> print_tree(unit_expr)
Mul: Msun/Mpc**3
+-Symbol: Msun
| comparable: False
+-Pow: Mpc**(-3)
+-Symbol: Mpc
| comparable: False
+-Integer: -3
real: True
...
When presented with a new unit specification string, a new Unit is created
by first decomposing the unit specification into atomic unit symbols. This may
require considering SI prefixes, which we allow for a whitelisted subset of
atomic unit symbols, listed in the table of unit symbols below. The Unit
instance is then created by combining a sympy expression for the unit and the
appropriate CGS factors, found by combining the CGS factors of the base unit and
optional SI prefixes.
Unit objects are associated with four instance members, a unit
Expression object, a dimensionality Expression object, a
UnitRegistry instance, and a scalar conversion factor to CGS units. These
data are available for a Unit object by accessing the expr,
dimensions, registry, and cgs_value attributes, respectively.
Unit provides the methods same_dimensions_as, which returns True if
passed a Unit object that has equivalent dimensions, get_cgs_equivalent,
which returns the equivalent cgs base units of the Unit, and the
is_code_unit property, which is True if the unit is composed purely of
code units and False otherwise. Unit also defines the mul, div,
pow, and eq operations with other unit objects, making it easy to
compose compound units algebraically.
The UnitRegistry class provides the add, remove, and modify
methods which allows users to add, remove, and modify atomic unit definitions
present in UnitRegistry objects. A dictionary lookup table is also attached
to the UnitRegistry object, providing an interface to look up unit symbols.
In general, unit registries should only be adjusted inside of a code frontend,
since otherwise quantities and arrays might be created with inconsistent unit
metadata. Once a unit object is created, it will not recieve updates if the
original unit registry is modified.
We also provide a singleton default_unit_registry instance that frontend
developers can copy and modify to build a simulation-specific unit symbol
registry.
The YTArray class works by tacking a Unit object onto an ndarray
instance. Besides the conversion methods already listed, most of the
implementation of YTArray depends on defining all possible ndarray
operations on YTArray instances. We want to preserve normal ndarray operations,
while getting the correct units on the resulting YTArray (be it in-place or
a copy). The proper way to handle operations on ndarray subclasses is explained
in the NumPy docs page, subclassing ndarray. We follow this approach and
describe the desired behavior in the next section below.
The code for these new classes will live in a new top-level yt.units
package. This package will contain five submodules:
unit_lookup_tableContains all static unit metadata used to generate the sympy unit system
unit_objectContains the
Unitclassunit_registryContains the
UnitRegistryclassyt_arrayContains the
YTArrayandYTQuantityclasses.unit_symbolsContains a host of predefined unit quantities, useful for applying units to raw scalar data.
Creating YTArray and YTQuantity instances¶
In the current implementation, there are two ways to create new array and quantity objects, via a constructor, and by multiplying scalar data by a unit quantity.
Class Constructor¶
The primary internal interface for creating new arrays and quantities is through
the class constructor for YTArray. The constructor takes three arguments. The
first argument is the input scalar data, which can be an integer, float, list,
or array. The second argument, input_units, is a unit specification which
must be a string or Unit instance. Last, users may optionally supply a
UnitRegistry instance, which will be attached to the array. If no
UnitRegistry is supplied, the default_unit_registry is used instead.
Unit specification strings must be algebraic combinations of unit symbol names,
using standard Python mathematical syntax (i.e. ** for the power function,
not ^).
Here is a simple example of YTArray creation:
>>> from yt.units import yt_array, YTQuantity
>>> YTArray([1, 2, 3], 'cm')
YTArray([1, 2, 3]) cm
>>> YTQuantity(3, 'J')
3 J
In addition to the class constructor, we have also defined two convenience
functions, quan, and arr, for quantity and array creation that are
attached to the StaticOutput base class. These were added to syntactically
simplify the creation of arrays with the UnitRegistry instance associated with
a dataset. These functions work exactly like the YTArray and YTQuantity
constructors, but pass the UnitRegistry instance attached to the dataset to
the underlying constructor call. For example:
>>> from yt.mods import *
>>> ds = load("Enzo_64/DD0043/data0043")
>>> ds.arr([1, 2, 3], 'code_length').in_cgs()
YTArray([ 5.55517285e+26, 1.11103457e+27, 1.66655186e+27]) cm
This example illustrates that the array is being created using
ds.unit_registry, rather than the default_unit_registry, for which
code_length is equivalent to cm.
Multiplication¶
New YTArray and YTQuantity instances can also be created by multiplying YTArray
or YTQuantity instances by float or ndarray instances. To make it easier to
create arrays using this mechanism, we have populated the yt.units namespace
with predefined YTQuantity instances that correspond to common unit symbol
names. For example:
>>> from yt.units import meter, gram, kilogram, second, joule
>>> kilogram*meter**2/second**2 == joule
True
>>> from yt.units import m, kg, s, W
>>> kg*m**2/s**3 == W
True
>>> from yt.units import kilometer
>>> three_kilometers = 3*kilometer
>>> print three_kilometers
3.0 km
>>> from yt.units import gram, kilogram
>>> print gram+kilogram
1001.0 g
>>> print kilogram+gram
1.001 kg
>>> print kilogram/gram
1000.0 dimensionless
Handling code units¶
If users want to work in code units, they can now ask for data in code units, just like any other unit system. For example:
>>> dd["density"].in_units("code_mass/code_length**3")
will return the density field in code units.
Code units are tightly coupled to on-disk parameters. To handle this fact of
life, the yt unit system can modify, add, and remove unit symbols via the
UnitRegistry.
Associating arrays with a coordinate system¶
To create quantities and arrays in units defined by a simulation coordinate
system, we associate a UnitRegistry instance with StaticOutput
instances. This unit registry contains the metadata necessary to convert the
array to CGS from some other known unit system and is available via
the unit_registry attribute that is attached to all StaticOutput
instances.
To avoid repetitive references to the unit_registry, we also define two new
member functions in the StaticOutput base class, quan and arr.
These functions simply pass the appropriate unit_registry object to the
YTQuantity and YTArray constructors, returning the resulting quantity or
array.
We have modified the definition for set_code_units in the StaticOutput
base class. In this new implemenation, the predefined code_mass,
code_length, code_time, and code_velocity symbols are adjusted to
the appropriate values and length_unit, time_unit, mass_unit,
velocity_unit attributes are attached to the StaticOutput instance. If
there are frontend specific code units, like MHD units, they should also be
defined in subclasses by extending this function.
Mixing modified unit registries¶
It becomes necessary to consider mixing unit registries whenever data needs to be compared between disparate datasets. The most straightforward example where this comes up is a cosmological simulation time series, where the code units evolve with time. The problem is quite general – we want to be able to compare any two datasets, even if they are unrelated.
We have designed the unit system to refer to a physical coordinate system based on CGS conversion factors. This means that operations on quantities with different unit registries will always agree since the final calculation is always performed in CGS.
The examples below illustrate the consistency of this choice:
>>> from yt.mods import *
>>> pf1 = load('Enzo_64/DD0002/data0002')
>>> pf2 = load('Enzo_64/DD0043/data0043')
>>> print pf1.length_unit, pf2.length_unit
128 Mpccm/h, 128 Mpccm/h
>>> print pf1.length_unit.in_cgs(), pf2.length_unit.in_cgs()
6.26145538088e+25 cm 5.55517285026e+26 cm
>>> print pf1.length_unit*pf2.length_unit
145359.100149 Mpccm**2/h**2
>>> print pf2.length_unit*pf1.length_unit
1846.7055432 Mpccm**2/h**2
Note that in both cases, the answer is not the seemingly trivial
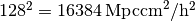 . This is because the new quantity
returned by the multiplication operation inherits the unit registry from the
left object in binary operations. This convention is enforced for all binary
operations on two YTarray objects. In any case, results are always consistent
in CGS:
. This is because the new quantity
returned by the multiplication operation inherits the unit registry from the
left object in binary operations. This convention is enforced for all binary
operations on two YTarray objects. In any case, results are always consistent
in CGS:
>>> print (pf1.length_unit*pf2.length_unit).in_cgs()
3.4783466935e+52 cm**2
>>> print pf1.length_unit.in_cgs()*pf2.length_unit.in_cgs()
3.4783466935e+52 cm**2
Handling cosmological units¶
We also want to handle comoving length units and the hubble little “h” unit. In
StaticOutput.set_units, we implement this by checking if the simulation is
cosmological, and if so adding comoving units to the dataset’s unit registry.
Comoving length unit symbols are still named following the pattern “(length
symbol)cm”, i.e. “pccm”.
The little “h” symbol is treated as a base unit, h, which defaults to unity.
StaticOutput.set_units should update the h symbol to the correct value
when loading a cosmological simulation.
LaTeX printing¶
We will make use of sympy’s LaTeX pretty-printing functionality to generate axis
and colorbar labels automatically for unit symbols. The LaTeX strings used for
atomic units are encoded in the latex_symbol_lut. This is necessary because,
for the purposes of LaTeX representation, sympy interprets symbol names as if
they were algebraic variables, and so get displayed using an italic font. Since
our symbols represent units, we want to display them in a roman font and need
to wrap them in \rm{}. New units do not need to be explicitly added to the
look-up-table, by default the LaTeX symbol will simply be the string name of the
unit, wrapped using \rm{}.
Using these LaTeX representations of atomic unit symbols, we then use sympy to generate labels, composing the LaTeX expressions for compound units according to the algebraic relationships between the atomic unit symbols.
YTArray operations¶
When working interactively, it is important to make sure quick workflows are
possible. To this end, we want to make it possible to use our new dimensionful
operations while still leveraging the syntactic simplicity NumPy offers. We want
to avoid mandating that all user-defined data be a YTArray or
YTQuantity.
To this end, we define operations between native Python objects like float,
NumPy float, NumPy ndarray, and YTArray. In the table below, we have
enumerated all combinations of YTArray, scalar (native Python float or
np.float64), and ndarray for binary operations. In most cases, unitful
operations are well defined, however in cases where the unitful operations are
not well defined, we raise a new exception, YTInvalidUnitOperation.
Since NumPy defines in-place, left, and right versions of all mathematical operations (i.e. add, iadd, ladd, radd), we only list the ‘basic’ version of each operation, with the expectation the implemenation accounts for all four variants, which all have the same behavior with respect to passing units.
| Operation | Combination | Result (pseudocode) |
|---|---|---|
| mul, div, truediv, floordiv | scalar, YTArray ndarray, YTArray | YTArray, units = input_units (op) 1
|
| YTArray, YTArray | YTArray, units = left_units (op) right_units
|
|
| add, sub | scalar, YTArray ndarray, YTArray | if YTArray is dimensionless:
return YTArray
|
| YTArray, YTArray | if left_units same dimensions as right_units:
return YTArray, in left_units
else:
raise YTInvalidUnitOperation
|
|
| pow | scalar, YTArray ndarray, YTArray |
if YTArray is dimensionless:
return scalar**YTArray
else:
raise YTInvalidUnitOperation
|
| YTArray, scalar | return YTArray**scalar (note units change)
|
|
| YTArray, ndarray | ||
| YTArray, YTArray | ||
| le, lt, ge, gt, eq | scalar, YTArray ndarray, YTArray | if YTArray is dimensionless:
return YTArray
else
raise YTInvalidUnitOperation
|
| YTArray, YTArray | if left_units same dimensions as right units:
return left (op) (right in left units)
else:
raise YTInvalidUnitOperation
|
| [1] | (1, 2) This one is a little tricky, since it is defined for ndarrays. Technically, it’s a well-defined unitful operation if the ndarray is the exponent. Unfortunately, this will make all the elements of the ndarray have different units, so we don’t allow it in practice. |
Now we list the behavior of unary operations on YTArray objects.
| Operation | Result (pseudocode) |
|---|---|
| abs, sqrt neg | YTArray |
| exp | if YTArray is dimensionless:
return exp(YTArray)
raise YTInvalidUnitOperation
|
Unit symbol names¶
In the table below we provide a listing of all units that are in the current implementation. We also list the dimensions of the unit, if the unit is in the whitelist to be prefixable with SI abbreviations, the dimensions of the unit, and the adopted CGS conversion factor.
| Unit | Symbol name | Dimensions | SI Prefixable? | CGS Conversion factor |
|---|---|---|---|---|
| Base units | ||||
| Gram | g | mass | yes | 1.0 |
| Meter | m | length | yes | 100.0 |
| Second | s | time | yes | 1.0 |
| Kelvin | K | temperature | yes | 1.0 |
| Radian | radian | angle | no | 1.0 |
| Gauss | gauss | magnetic_field | yes | 1.0 |
| Code units | ||||
| Code mass units | code_mass | mass | no | ? |
| Code length units | code_length | length | no | ? |
| Code time units | code_time | time | no | ? |
| Code velocity units | code_velocity | velocity | no | ? |
| Code magnetic field units | code_magnetic | magnetic_field | no | ? |
| Code temperature units | code_temperatre | temperature | no | ? |
| Code metallicity units | code_metallicity | metallicity | no | ? |
| Normalized domain units | unitary | length | no | Domain width |
| Misc CGS | ||||
| Dyne | dyne | force | yes | 1.0 |
| Erg | erg | energy | yes | 1.0 |
| Electrostatic unit | esu | (energy*length)**0.5 | yes | 1.0 |
| Gauss | gauss | magnetic_field | yes | 1.0 |
| Misc SI | ||||
| Joule | J | energy | yes | 1.0e7 |
| Watt | W | power | yes | 1.0e7 |
| Hertz | Hz | rate | yes | 1.0 |
| Imperial units | ||||
| Foot | ft | length | no | 30.48 |
| Mile | mile | length | no | 160934 |
| Cosmological “units” | ||||
| Little h | h | dimensionless | no | ? |
| Time units | ||||
| Minute | min | time | no | 60 |
| Hour | hr | time | no | 3600 |
| Day | day | time | no | 86400 |
| Year | yr | time | yes | 31557600 |
| Solar units | ||||
| Solar mass | Msun | mass | no | 1.98841586e33 |
| Solar radius | Rsun | length | no | 6.9550e10 |
| Solar luminosity | Lsun | power | no | 3.8270e33 |
| Solar temperature | Tsun | temperature | no | 5870.0 |
| Solar metallicity | Zsun | metallicity | no | 0.02041 |
| Astronomical distances | ||||
| Astronomical unit | AU | length | no | 1.49597871e13 |
| Light year | ly | length | no | 9.4605284e17 |
| Parsec | pc | length | yes | 3.0856776e18 |
| Angles | ||||
| Degree | degree | angle | no | 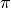 /180 /180 |
| Arcminute | arcmin | angle | no | 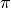 /10800 /10800 |
| Arcsecond | arcsec | angle | no | 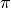 /648000 /648000 |
| Milliarcsecond | mas | angle | no | 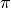 /648000000 /648000000 |
| Physical units | ||||
| Electron volt | eV | energy | no | 1.602176562e-12 |
| Atomic mass unit | amu | mass | no | 1.660538921e-24 |
| Electron mass | me | mass | no | 9.10938291e-28 |
Testing¶
We have written a set of unit tests that check to make sure all valid and invalid unit operations succeed or fail as appropriate. We will also need to verify that the extant unit and answer tests pass before this can be accepted.
Backwards Compatibility¶
This is a serious break in backwards compatibility. Once this is accepted,
units will no longer be stored in the StaticOutput dict. This means that all
scripts which use the pf[unit] construction will no longer be valid. We will
also need to eliminate instances of this construction within the yt codebase.
We will need to check to make sure the analysis modules and external tools that
operate on yt data can either work appropriately with YTArray or figure out a
way to degrade to ndarray gracefully.